Security is only as good as the weakest link.
Example: You have installed a very strong lock on your front door. A potential intruder will look at the strong lock and go to the back of the house and find a weaker lock to pick.
Also, one should be able to quantify what a "very strong lock" means. If you go to Home Depot and see two locks, one that says "super strong" and the other "ultimate strength", it does not help you much. But if one said "it will take an experienced lock picker 1 hr to pick it based on govt. lock-picking standard xyz", it gives you a way to compare 2 locks. Fortunately, when it comes to cryptography, one can quantify the strength of an algorithm.
Bits of Security
An algorithm has an associated bits of security. 128 bits of security is considered good and it is infeasible for an attacker to break it. If a crypto algorithm has effective security of 128 bits, then it is fine.
Encryption
When you use your browser to login to your bank, the messages are encrypted. Both your browser and the bank web-server will use the same encryption key, so that the browser can encrypt the message with the encryption key and the web-server can decrypt it with the same key and vice-versa. As the same key is used for encryption and decryption, it is called symmetric encryption.
We will skip the part, for now, about how the browser and web-server can be in possession of the same encryption key.
The encryption algorithm used is typically AES-128-GCM. The 128 refers to the size of the key in bits. For this algorithm, it turns out that 128 bit key provides 128 bits of security and this, as we said earlier, is more than adequate.
AES-256-GCM, which has a key size of 256 bits and provides 256 bits of security, is also widely used. Though 256 bits of security is more than the required 128 and is an overkill, it looks good in marketing literature.
Note: key size of b-bits doesn’t always imply b-bits of security — depending on the algorithm, you may get bits of security much less than the key size.
AES-xxx-GCM algorithm performs encryption and authentication together and it belongs to a class of algorithms called Authenticated-Encryption algorithms. There is an older or legacy encryption algorithm called AES-CBC which only does encryption and so it has to be combined with an authentication algorithm called a MAC. The encryption HAS to be done before authentication (MAC) but some early protocols between the browser and web-server got it wrong, by doing the opposite and so were vulnerable to a class of attacks called padding-oracle attacks.
Encryption — quantum-safe
In the previous section, I mentioned that 256 bits of security for encryption is an overkill. This is true — 128 bits of security is more than enough. But this refers to classical computing. There is a new class of computing called quantum computing. Currently it is in very early stages and it may be several years if not decades before this is practical. More than 20 years ago, Grover published a quantum search algorithm that gives a quadratic speedup in finding the encryption key.
With Grover’s algorithm, AES-128 has only 64 bits of security and AES-256 has only 128 bits of security.
This is a conservative estimate as Grover’s algorithm requires a long-running serial computation, which is difficult to implement in practice.
Though we have Grover’s algorithm, we don’t have a quantum computer capable of running it for the key sizes in use. But we can play it safe and use AES-256 instead of AES-128.
Summary: AES-256 is quantum safe as it provides 128 bits of security even with Grover’s search algorithm.
Hashing — quantum safe
Hashing algorithms like SHA2 and SHA3-256 are quantum safe. No need to worry.
Key exchange
For encryption to work, the browser and web-server (or the 2 parties in a Whatsapp chat) need to have the same encryption key. Also, this shared-key should be changed frequently. How is this possible?
The recommended way of doing this is via a process called a key-exchange.
There are 2 algorithms for Key Exchange:
1) Diffie-Hellman (DH) Key Exchange — key size more than 3000 bits
2) Elliptic curve Diffie-Hellman (ECDH) Key Exchange — key size of at least 256 bits
The 2 parties exchange key material that can then be used to compute the same encryption key. Though the key materials are exchanged in the clear over an insecure channel, and any one can see it, no one other than the 2 parties can compute the shared-key: the attacker has to solve the discrete logarithm problem (in the case of DH Key Exchange) or elliptic curve discrete logarithm problem (in the case ECDH Key Exchange) to compute the shared-key and they are very hard problems. These 2 problems will be refereed to as DLP and ECDLP.
Signatures
Though key exchange can be performed over an insecure channel and no one other than the 2 parties — say Alice and Bob — can compute the shared key, the key exchange algorithms don’t prevent a man-in-the-middle (MitM) — say Charlie — from impersonating. Alice and Bob think that they are exchanging key material with one another when in fact they are exchanging them with Charlie.
Though one cannot easily prevent the MitM, it can be detected by digitally signing the key material before sending it to the other party. The party receiving the key material can verify that the signature is valid — if it is not, it is rejected.
There are 3 algorithms for signing:
1) RSA — based on the difficulty of factoring huge numbers — key size more than 3000 bits
2) DSA — based on difficulty of the discrete logarithm problem (DLP) — key size more than 3000 bits
3) ECDSA — based on difficulty of elliptic curve discrete logarithm problem (ECDLP) — key size of at least 256 bits
Strength of Encryption, Key Exchange and Signature algorithms — classical
Recall that 128 bits of security is enough and that key size of b-bits doesn’t necessarily imply b-bits of security.
In the case of Diffie-Hellman (DH) Key Exchange algorithm and DSA Signature algorithm — both of which depend on the difficulty of the discrete logarithm problem (DLP) — and the RSA signature algorithm, I listed a key size of more than 3000 bits.
The reason is that there is a powerful algorithm called general number field sieve (GNFS) that solves the finite field discrete logarithm problem and integer factoring problems in sub-exponential time.
Due to GNFS, a key size of at least 3000 bits is required for Diffie-Hellman Key Exchange and Signature algorithms.
In the cae of Elliptic curve Diffie-Hellman (ECDH) Key Exchange and ECDSA signature algorithms, both of which are based on difficulty of elliptic curve discrete logarithm problem (ECDLP), a much harder problem, a key size of 256 bits is enough to get 128 bits of security. Smaller key sizes is one of the reasons elliptic curve cryptography is currently preferred — also works well on memory constrained devices like mobile phones.
Remember the first sentence in this blog article: Security is only as good as the weakest link — if your s/w uses encryption, key exchange and digital signatures, you need to ensure that all have at least 128 bits of security.
| Category | Algorithm | Key size (bits) | Bits of Security |
|---|---|---|---|
| Encryption | AES | 128 | 128 |
| Key Exchange | Diffie Hellman (DH) | 3000 | 130 |
| Signature | DSA | 3000 | 130 |
| Signature | RSA | 3000 | 130 |
| Key Exchange | Elliptic Curve DH | 256 | 128 |
| Signature | ECDSA | 256 | 128 |
GNFS algorithm
As mentioned earlier, GNFS algorithm solves the finite field discrete logarithm problem and integer factoring problem with a runtime sub-exponential to the size (in bits) of the input.
The correspondence between the length of a Diffie-Hellman or RSA key and the length of a symmetric key of an identical strength can be computed using the following hairy equation:
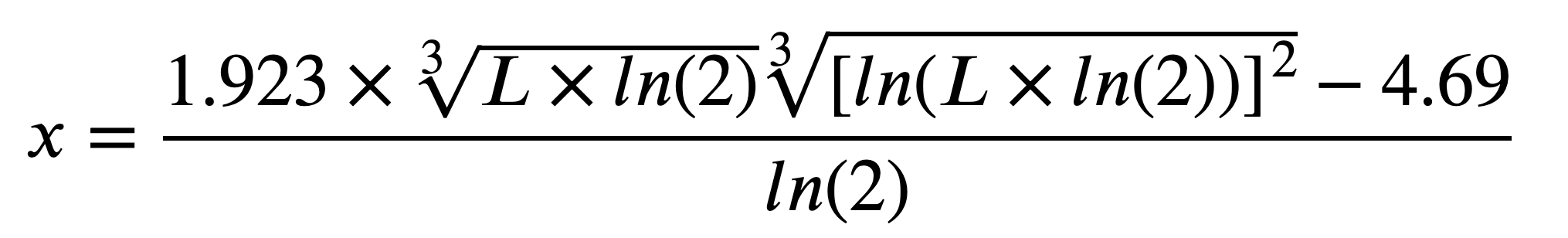
The table below shows the bits of security when GNFS algorithm is used to solve the discrete logarithm and integer factoring problems.
| Key size (bits) | Bits of Security |
|---|---|
| 1024 | 79 |
| 2048 | 110 |
| 2900 | 128 |
| 3000 | 130 |
| 3072 | 131 |
| 4096 | 149 |
| 8192 | 201 |
| 14446 | 256 |
| 16384 | 269 |
Quantum Computing breaks public key encryption, key exchange and signatures
Over 20 years ago, American mathematician Peter Shor published a paper that solves public key encryption, key exchange and signatures much much faster — in polynomial time instead of sub-exponential, effecting breaking them. These problems are trivial for a quantum computer. This applies to elliptic key cryptography also.
The saving grace, of course, is that we do not have a quantum computer — this may be years or decades away.
A quantum computer has quantum bits (qubits). The state of the art is a quantum computer with 65 qubits. Conservative estimate is that we would need a quantum computer with millions of qubits to factor a 2048 bit number.
Strength of Encryption, Key Exchange and Signature algorithms — quantum
Let us update the table assuming quantum computers are available now.
| Category | Algorithm | Key Size (bits) | Bits of Security | with Quantum Computers |
|---|---|---|---|---|
| Encryption | AES | 128 | 128 | 64 bits (very weak) |
| Encryption | AES | 256 | 256 | 128 |
| Key Exchange | Diffie Hellman (DH) | 3000 | 130 | broken |
| Signature | DSA | 3000 | 130 | broken |
| Signature | RSA | 3000 | 130 | broken |
| Key Exchange | Elliptic Curve DH | 256 | 128 | broken |
| Signature | ECDSA | 256 | 128 | broken |
Post Quantum Cryptography — public key encryption, key exchange and signatures
Though practical quantum computers may not be available for several decades, one should not be complacent. What if this estimate is wrong? So, there is lot of research in the area of post-quantum cryptography to come up with quantum-resistant or quantum-safe crypto algorithms.
Categories
The post quantum algorithms depend on problems that are hard even for quantum computers. They can be classified as follows:
-
Lattice based — encryption and signatures (1998)
hard problem: Find shortest vector, closest vector in lattice. -
Code based — encryption and signatures (1978)
hard problem: Decode random linear code.Drawback: large public key (1 megabyte)
-
Isogeny based — encryption
hard problem: Find isogeny map between elliptic curves with same number of points -
multivariate based — encryption and signatures (1996)
hard problem: solve multivariate quadratic equations over finite fields -
Hash based — Signatures (1979)
hard problem: Second pre-image resistance of hash function
NIST: Post Quantum Crypto competition
In the past, NIST used a competition to select the ‘best’ symmetric encryption and hashing algorithms and chose Rijndael Encryption Algorithm (AES) and SHA3 hashing algorithm.
3 years ago, NIST requested nominations for public-key post-quantum cryptographic algorithms. Winners will be selected in 2023. There were 69 entries in the first round, 26 in the second round and as of July 2020, we are in the third round with 15 entries remaining — 7 finalists and 8 alternates.
NIST says that while "perfect forward secrecy’ is desirable, it will not be used for evaluation. It says, "While this property can be obtained through the use of standard encryption and signature functionalities, the cost of doing so may be prohibitive in some cases".
The cryptographer Daniel Bernstein says that "Diffie-Hellman is hard to do post-quantum".
NIST 3rd round finalists (July 2020)
-
Public key encryption, key encapsulation
a. Classic McEliece (Code based)
b. CRYSTALS-KYBER (Lattice based)
c. NTRU (Lattice based)
d. SABER (Lattice based) -
Digital signature algorithm
a. CRYSTALS-DILITHIUM (Lattice based)
b. FALCON (Lattice based)
c. Rainbow (Multivariate)
Summary
A lot of our data at rest is protected with AES-128 symmetric key encryption. To be quantum-safe, sensitive data can be re-encrypted with AES-256; new data can be encrypted with AES-256.
Out of the 69 algorithms submitted by researchers, many were found to be vulnerable. Researchers will be trying to find vulnerabilities in the 15 remaining algorithms.
In 2023, NIST will select couple of public key encryption, key encapsulation algorithms and couple of Digital signature algorithms. Also, given that 6 years would have elapsed since the initial request for algorithms, NIST will find a way to look at newer approaches too.
Once we have well tested implementations of the selected quantum resistant public key algorithms, we can rest easy. We can watch with fascination the progress made in quantum computing as it is able to factor larger and larger numbers, solve larger finite field and elliptic key cryptography problems.
