Snow3G is one of the two algorithms (the other being AES) algorithms used in LTE (4G) mobile network. The specifications for LTE come from the standards body called 3GPP and include the specification and reference implementation in C for the Snow 3G algorithm. There is an algorithm for confidentiality (encryption/decryption), and an algorithm for integrity.
The Snow3G confidentiality algorithm (also called f8) is a stream cipher that is used to encrypt/decrypt blocks of data under a 128 bit confidentiality key and IV (initialization vector). A stream cipher essentially generates a (pseudo) random sequence of bits of length equal to the length of the input, and the encrypted output is the xor (exclusive or) of the random sequence and the input. Snow3G is a word-oriented stream cipher as it outputs 32 bits at a time.
The Snow3g integrity algorithm (also called f9) computes a 32-bit MAC (Message Authentication Code) of a given input message using an 128 bit integrity key and IV.
The Snow3G algorithms use a 16 stage 32 bit LFSR (Linear Feedback Shift Register), s0 to s15 that feed a 3 register FSM (Finite State Machine), R1 to R3.
LFSR is a shift register whose input bit is a linear function of its previous state — the feedback is a primitive polynomial over the finite field. The feedback function is carefully chosen to produce a sequence of (pseudo) random bits with a very long cycle.
FSM uses two boxes S1 and S2 which are 32-bit to 32-bit substitutions. That is, S1 :: Word32 -> Word32 and S2 :: Word32 -> Word32
This algorithm, which requires shifting and updating values in registers, can be easily and efficiently implemented in traditional non-functional languages (imperative style) where mutability allows for changing state — an array can be used to represent LSFR and FSM and updates can be made in place. In a pure functional programming language like Haskell, data is immutable — when you update an array you get a new array and this means that algorithms that make critical use of updatable state will be very inefficient.
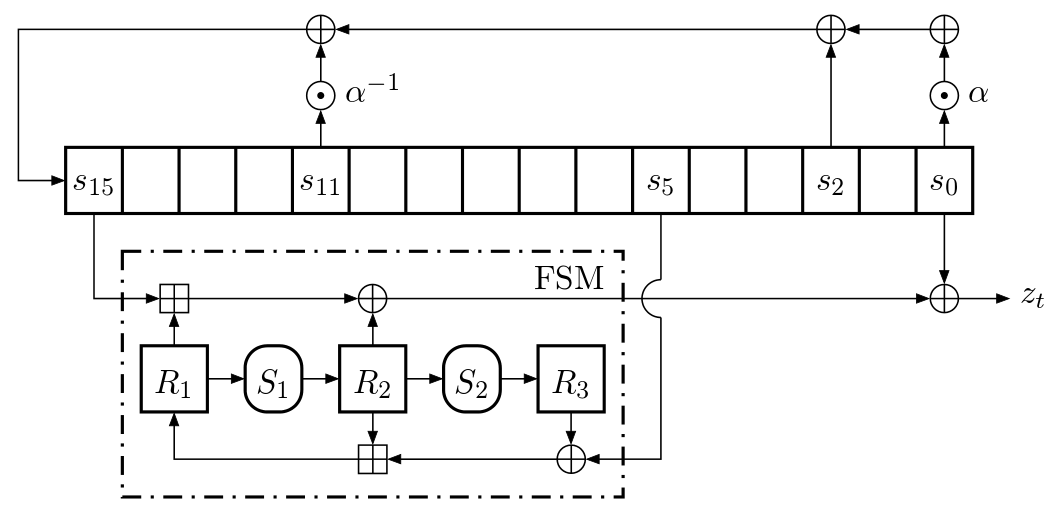
Figure 1: Snow3g keystream mode
However, we know that the Snow3G algorithm is a pure function — it is a deterministic algorithm where for the same input, you get the same output. So, the function signatures for ciphering and integrity should be
snowCipher :: CipherKey -> CipherInput -> String
snowIntegrity :: CipherKey -> CipherInput -> Word32Question: In a purely functional language Haskell, is it possible to have an external specification that is purely functional (as shown above), while the internal implementation makes use of updatable state? Can Haskell’s type system be used to securely encapsulate stateful computations? The answer is yes. The 1993 (yes, 1993!) paper titled Lazy Functional State Threads by John Launchbury , Simon L. Peyton Jones showed how to achieve this using primitives for mutable arrays and a State Transformer (ST) Monad. Note that in order to ensure that the stateful computation is securely encapsulated, rank-2 polymorphism is required. The GHC compiler implements the ST Monad.
After all the stateful computations are done, we need to ‘escape’ from the ST monad to get a pure function by invoking the runST function whose signature is runST :: ST s a -> a. As mentioned in the paper, "runST takes a state transformer as its argument, conjures up an initial empty state, applies the state transformer to it, and returns the result while discarding the final state"
For this Snow3G implementation, an unboxed mutable array is used to represent the 16 stage, 32 bit LFSR and the 3 registers of FSM. runSTUArray provides a safe way to create and work with this unboxed mutable array before returning an immutable array (without copying). Its signature is
runSTUArray :: (forall s. ST s (STUArray s i e)) -> UArray i e |
Here is code Snippet for the snowCipher:
snowCipher :: CipherKey -> CipherInput -> String snowCipher cipherKey cipherInput = let cipherOutput = snowCipher_ cipherKey cipherInput in concat [printf "%08x" b | (_, b) <- Data.Array.Base.assocs cipherOutput] snowCipher_ cipherKey cipherInput = runSTUArray $ do lfsr_fsm <- newSTUArray (0, lfsr_fsm_length-1) (0::Word32) cipherOutput <- newSTUArray (0, numWord32-1) (0::Word32) initialize_ key iv lfsr_fsm sequence [do xorf <- liftM xor (getStreamWord32_ lfsr_fsm) writeArray cipherOutput i $ xorf (inputWord32 ! i) | i <- [0 .. numWord32-1]] when (mask > 0) $ do lastWord <- readArray cipherOutput (numWord32-1) writeArray cipherOutput (numWord32-1) $ lastWord .&. mask return cipherOutput where num_lfsr_stages = 16 num_fms_registers = 3 lfsr_fsm_length = num_lfsr_stages + num_fms_registers cipherInputOctets = hexStringToOctets (hexInput cipherInput) inputWord32 = getWord32WithPaddingV cipherInputOctets numWord32 = Data.Vector.Unboxed.length inputWord32 key = splitKeyV $ _keyHex cipherKey count = _count cipherKey bearer = _bearer_or_fresh cipherKey dir = _dir cipherKey iv = fromList [(bearer <code>shiftL</code> 27) .|. ((dir .&. 0x1) <code>shiftL</code> 26), count, (bearer <code>shiftL</code> 27) .|. ((dir .&. 0x1) <code>shiftL</code> 26), count] lbits = inputLengthInBits cipherInput mask = if (lbits <code>mod</code> 32) > 0 then complement $ ((1::Word32) <code>shiftL</code> (32 - (lbits <code>mod</code> 32))) - 1 else (0::Word32) |
It would be nice if there is a way to demonstrate this Snow3G algorithms in a web app — yes there is!. The amazing ghcjs can take any Haskell code or library (except those that have underlying native code dependencies) and convert it into Javascript. See my related blog article on the javascript problem. For the web UI portion, there are many options: I have used the powerful Functional Reactive Programming (FRP) system called reflex and a dom framework built on top of it.
You can checkout my Snow3G crypto here: https://blog.srinivasan.biz/ghcjs/snow3g/
